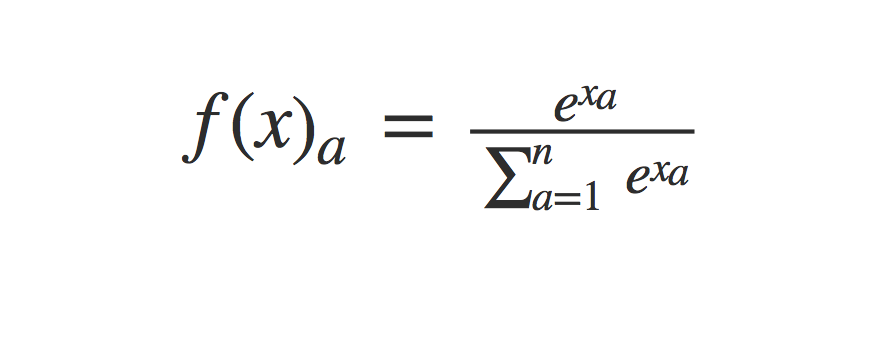Activation Functions

A Deeper Understanding By: Adam Lieberman

What is an Activation Function?

An activation function is a mathematical function that is applied to the linear combination of weights and input values within a node in a hidden layer.

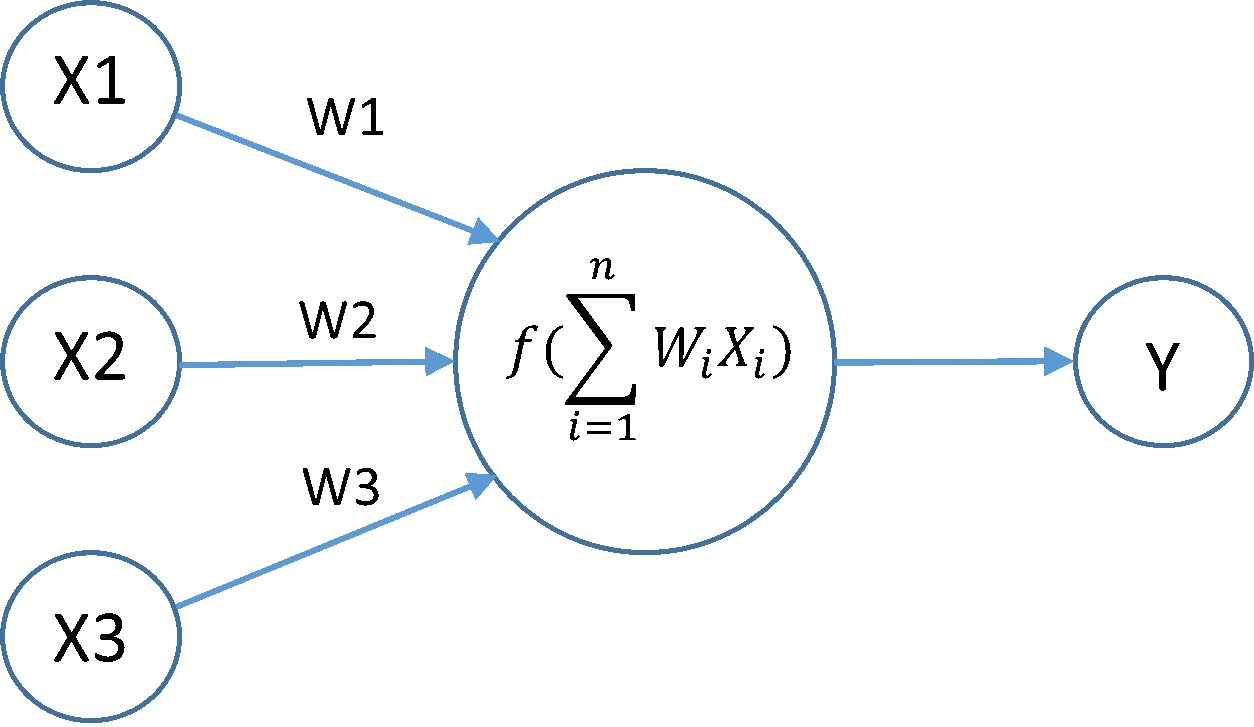
Above we see that we have the input values $X1, X2, X3$ and the weights $W1, W2, W3$. There is one hidden layer with one node. In this node we take the linear combination of the inputs and weights to calculate

$$\sum_{i=1}^3W_iX_i = W1X1 + W2X2 + W3X3$$

Additionally, there is a bias term added to this linear combination. This allows the neural network to translate its decision boundary. If we let our bias be denoted as $b_1$ in the above example then our neuron in the hidden layer computes

$$W1X1 + W2X2 + W3X3 + b_1$$

We see that the above quantity is linear. However, there is a good chance that our dataset is non-linear and we want to learn a non-linear mapping between our inputs and targets. To introduce this non-linearity into the network, we apply a mathematical operation $f$, known as an activation function, on the computed linear combination. Applying this activation function leaves us with the following quantity

$$f\left(W1X1 + W2X2 + W3X3 + b_1\right)$$

There are many different activation functions used, each with their own formulas, properties, pros, and cons. Understanding these functions at a mathematical level allows one to properly identify which activation functions to use in their deep learning models.

The Standard Activation Functions

Below are the names and formulas for some very popular activation functions used in deep learning:

Linear

$f(x)=x$

Sigmoid

$f(x)=\frac{1}{1+e^{-x}}$

Tanh

$f(x)=\frac{2}{1+e^{-2x}-1}$

ReLU

$f(x) = max(0,x)$

Leaky ReLU

$f(x)=max(x,k\cdot z)$

$0 < k < 1$

Softmax

$f(x)_a = \frac{e^{x_a}}{\sum_{a=1}^ne^{x_a}}$

Below are plots of the activation functions with their respective derivatives:

Linear

Sigmoid

tanh

ReLu

Leaky ReLu

Softmax

Let us now dive into each of the above activation functions and examine them at a deeper level:

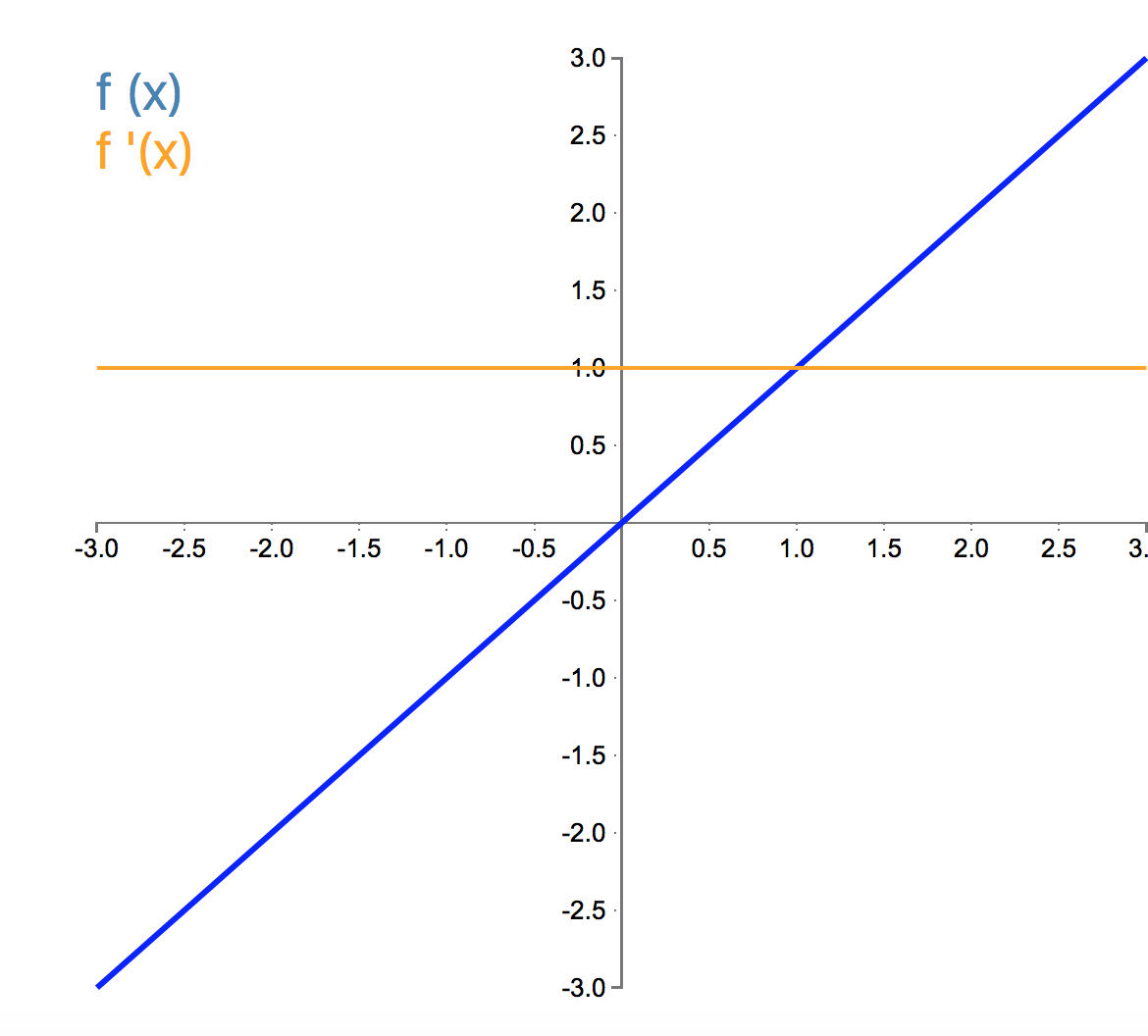
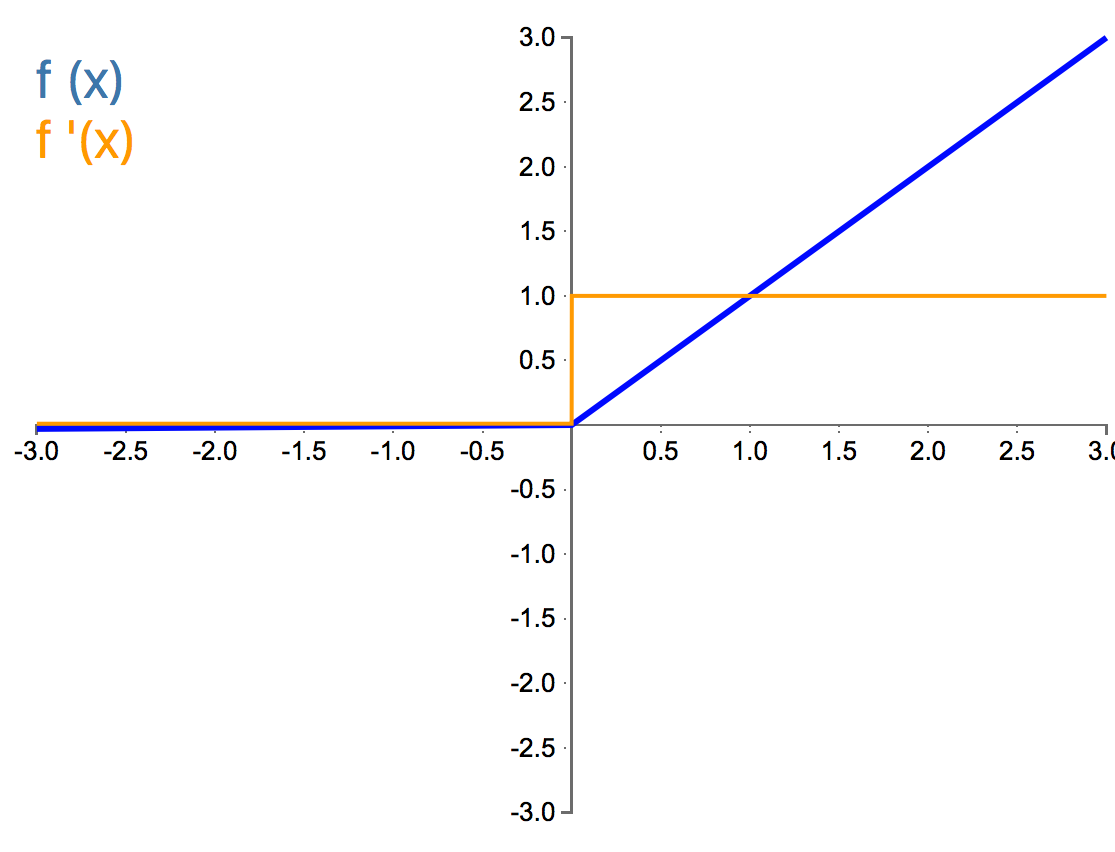
The Linear:

Properties:

The Linear activation function is a function which produces a node output equal to its input. It is a linear and monotonic function that has range $-\infty$ to $\infty$.

Drawbacks:

Non-Linearity - The linear function is insufficient when non-linearities are present in the data.

Benefits:

No Vanishing Gradient - There is no vanishing gradient with a linear activation function.
No Exploding Gradient - There is no exploding of the gradient with a linear activation function.
No Saturated Neurons - There is no saturated neurons with a linear activation function.
No Dead Neurons - There are no dead neurons with a linear activation function.

Conclusion:

The linear activation function is perfectly suited to tasks where we have a linear behavior in our data. We typically use a linear activation in the output layer of our neural network if we have a regression problem. The linear activation is not commonly used in the hidden layers.

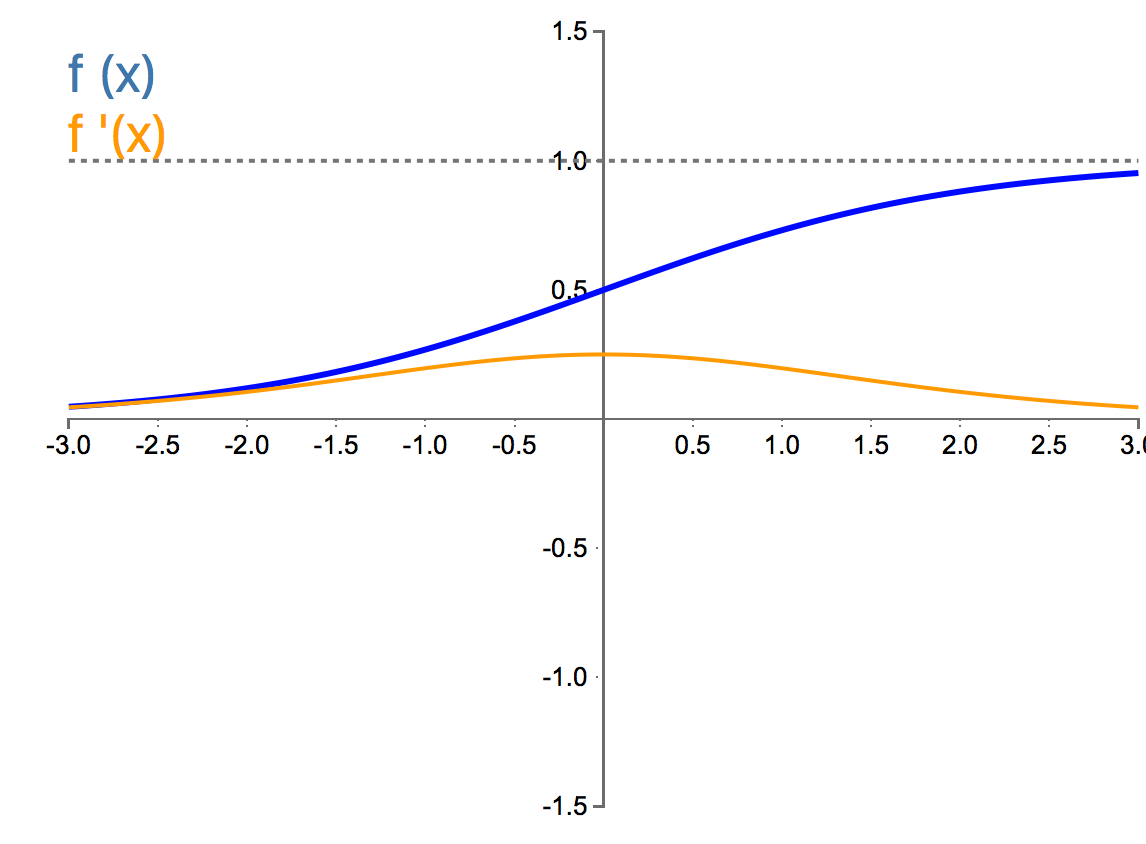
The Sigmoid:

Properties:

The sigmoid is a smooth and non-linear continuously differentiable function that squashes real numbers to range between 0 and 1. It has an S shaped curve that is monotonic. Additionally, the sigmoid is asymmetrical around the origin.

Drawbacks:

Vanishing Gradient - When we apply a large negative to the sigmoid we get close to a 0 value. When we apply a large positive to the sigmoid we get close to a 1 value. If we look at the gradients at these tail regions we see that we effectively have a 0 value. During back propagation we multiply the local gradient to the gradient of the previous gate's output. If we have a small local gradient we will have a vanishing gradient and will thus have no signal for weight update. Thus, the sigmoid function suffers from the vanishing gradient problem as the learning process stops and the weights stop updating with increasing epochs as the gradient has fallen to 0. There needs to be a nonzero gradient for the weights to be updated.
Saturated Neurons - When we initialize the weights to our network we have to be careful. If our weight initialization is too large then most neurons become saturated thus not allowing the network to properly learn. This can cause class imbalance irrespective of the input sample.
Non-Zero Centered Outputs - Since our range is between 0 and 1 we always have positive data coming into the next neuron. This will cause the gradient on the weights to become all positive or all negative during back propagation.

When we apply a large negative number to the sigmoid we get a 0 value and when we apply large positive numbers to the sigmoid we get a 1. When we look at these extreme tail regions we see that the gradient is almost 0. As we apply sigmoid after sigmoid we see that

Benefits:

No Exploding Gradients - The sigmoid function does not cause an explosion in gradients when activation after activation function is applied. We see that the maximum range the function can take on is 1 after the sigmoid is applied and that the derivative peaks out at the range 0.25 for any real number so the gradients will never explode in magnitude.

Conclusion:

The sigmoid function has been widely used for a long time. In general it was used for cases where we are predicting the probability as an output since it outputs values in the range of 0,1 and probabilities only exist between this range. The probabilities from the sigmoid do not always sum to one so using this activation function can be useful in cases where there are multiple true answers instead of one correct classification or multi-class classification. For instance, we would want to use the sigmoid function in the output layer if we showed a network a picture that contained multiple cars and humans. Here we would want the network to produce a probability that each car was a car and that each human was a car. Here we do not need all the probabilities to sum to 1. This would allow us to detect the multiple cars in the image and discern them from the people in the image. We would not want to use the sigmoid if we have a multi-class classification problem where there was just one correct answer for which class is present in the image or data. For instance, we would not use the sigmoid to determine if an image is a cat or a dog or a bird, since we would desire the output probability to sum to one, thus not making it a probability distribution. There is an alternate activation function called the softmax which performs this, thus the sigmoid is not desirable in the case of a multi-class classification problem. However, if we have a binary classification problem the sigmoid and softmax will perform equally well with the sigmoid function being a more simple operation. Additionally, we would not use the sigmoid activation function in the output layer for a regression problem since we would desire an unbounded range and the sigmoid is constrained between the range of 0 to 1. Thus, if the sigmoid is used it is used in the output layer if we are seeking the probability of multiple "true" answers such as the presence of various objects in an image. Additionally, we could use it for the output layer in a binary classification problem. However, it should most likely not be used in hidden layers.

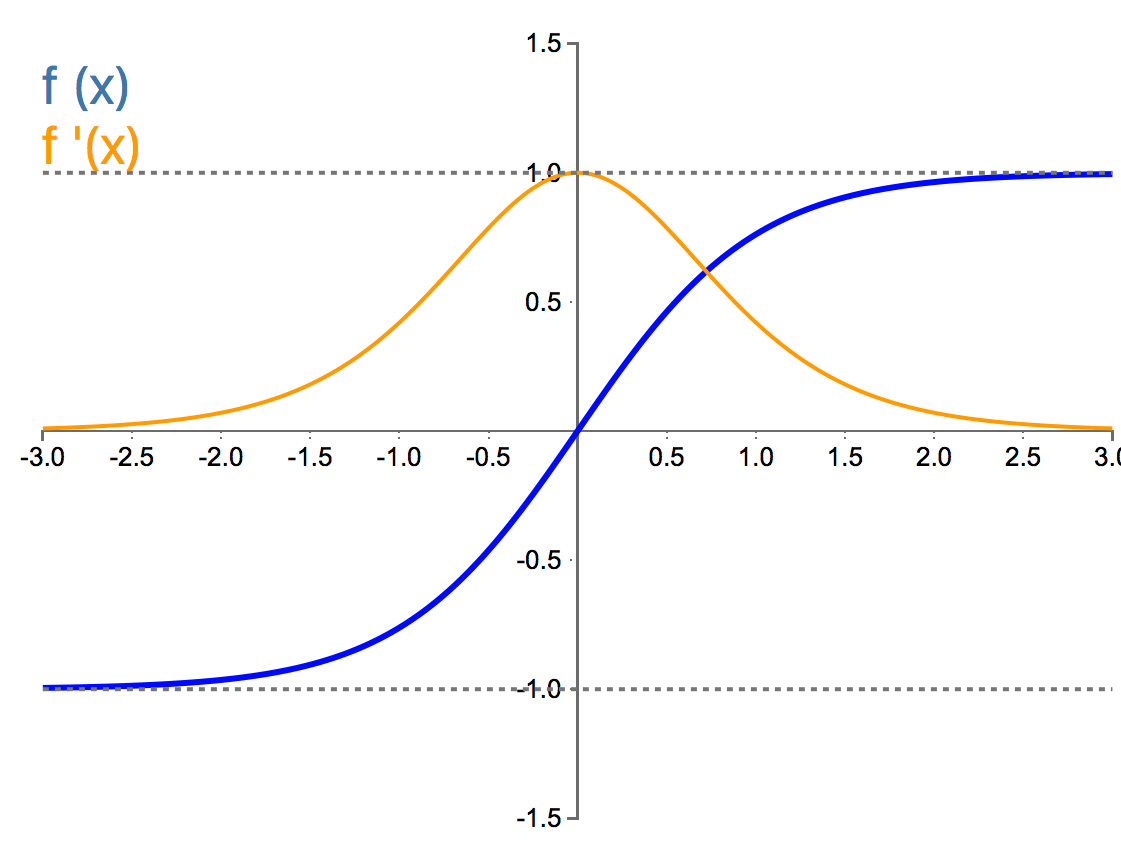
The Tanh:

Properties:

The hyperbolic tangent, or tanh, is a smooth and non-linear continuously differentiable function that squashes real numbers to range between -1 and 1. It has an S shaped curve that is monotonic.The tanh function is mathematically a shifted version of the sigmoid function such that it goes through the origin, making it zero-centered.

Drawbacks:

Vanishing Gradients - Like the sigmoid, the tanh has the problem of vanishing gradients.
Saturated Neurons - Like the sigmoid, the tanh has the problem of saturated gradients.

Benefits:

Hidden Units - For hidden units, the tanh almost always works better than the sigmoid function because we produce values between -1 and 1 compared to values between 0 and 1. Here, the mean of the activations that come out of the hidden layers are closer to having a zero mean. This allows us to have stronger gradients since the data is centered around 0 which makes the derivatives higher. If we look at the derivative of the sigmoid function we see we take on a range between 0 and 0.25. With the tanh's derivative we take on values between a range of 0 and 1. The tanh non-linearity is usually always preferred to the sigmoid nonlinearity.
No Exploding Gradients - Like the sigmoid, the tanh does not have the problem of exploding gradients.

Conclusion:

The tanh is preferred to the sigmoid when we are choosing what activations we should use in the hidden layers and this is highly due to the zero-centered activation value property. It is still not as desirable as some alternate activation function called the ReLu but is preferred over the sigmoid. The tanh should not be used in the output layer if an output probability is desired as it produces values in the range -1 to 1 not 0 to 1 like the sigmoid. It can be used to discern classes in a binary classification problem as negative values can learn more towards one class and positive values can learn more towards another class. However, for classification tasks the softmax activation is preferred with the sigmoid trailing behind it. In summary, the tanh is preferred to the sigmoid for use in the hidden layers but for classification and regression problems it is not as desirable for use in the output layer.

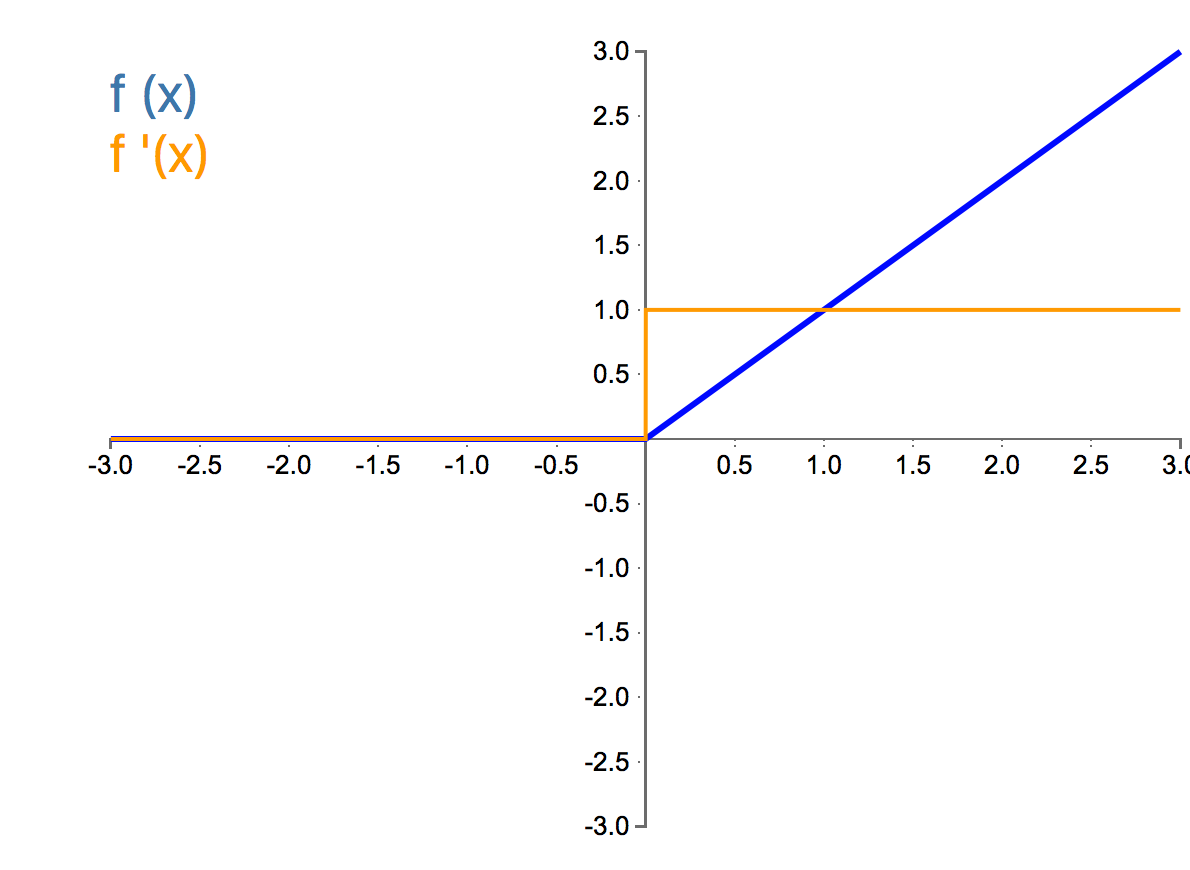
The ReLU:

Properties:

The rectified linear unit, or ReLu, is a piece-wise linear function. It has range 0 to $\infty$ and is monotonic. Additionally it is Asymmetrical. It has non-zero derivative at positive inputs and zero derivative at non-positive inputs. The ReLU is simply a threshold at zero.

Drawbacks:

Dead Neurons - During training, ReLU units can die. If we have a large gradient that is flowing through a ReLU neuron this can cause the weights to update in a way such that the neuron will never activate on any data point again. This will cause the gradient to forever be zero from that point on and the weights to not be updated during gradient descent. The sigmoid and tanh functions at least always have a small gradient allowing them to recover in the long term. Once the neuron dies with a ReLU it is very hard to recover.

Benefits:

No Vanishing Gradient - The ReLU has no vanishing gradient problem like the sigmoid or tanh. This is because the gradient is either 0 or 1, which means it never saturates, and so gradients cannot vanish — they are transferred perfectly across the network.
No Exploding Gradient - The ReLU does not explode the gradient.
No Saturated Neurons - The ReLU does not produce saturated neurons. It also has a linear form that speeds up the convergence of stochastic gradient descent compared to the sigmoid and tanh functions.
No Complex Mathematical Operations - Compared to the sigmoid or tanh activation functions, the ReLU does not involve complex operations like exponentials. It is a simple operation by simply thresholding a matrix of activations at zero.

Conclusion:

The ReLU is the most common activation function chosen to be used inside hidden layers. It is generally better to use than the sigmoid or tanh functions in the hidden layers. If one is confused with what activation function to use in the hidden layers, the ReLU is a great first choice. ReLU activation functions should only be used in the hidden layers as we prefer output layers to have softmax activations for classification problems (or sigmoid for binary classification) and regression problems to have a linear activation on the output layer.

The Leaky ReLU:

Properties:

The Leaky ReLU is a ReLU function that drops slightly below the x axis for negative values (usually scaling $x$ by $0.01$ for $x < 0$), this having a very small slope for these negative value inputs. Just like the ReLU it is a piece-wise linear function that is monotonic and asymmetrical. It has range $-\infty$ to $\infty$.

Drawbacks:

Vanishing Gradient - The Leaky ReLU does have the problem of a vanishing gradient.

Benefits:

No Dead Neurons - The Leaky ReLU has a small negative slope for negative valued inputs. Thus, we have at least some small gradient and fix the dying neuron problem.

No Exploding Gradient - Like the ReLU, there is no exploding gradient.

No Saturated Neurons - Like the ReLU, there is no exploding gradient.

Conclusion:

The Leaky ReLU is a good choice for hidden layer units if one experiences a vanishing gradient. In general the ReLU is used more often in the hidden layers compared to the Leaky ReLU. The Leaky ReLU is not used in the output layers for classification and regression probelms.

The Softmax:

The softmax is a logistic function with the condition that the probabilities values from the application of the softmax must sum to 1. This makes it highly desirable for the output layer in a multi-class or binary classification problem. The softmax is generally not used in hidden layers as it can introduce linear dependence on our nodes which can result in problems. However, a softmax can be used in the hidden layer if we are building an attention mechanism.

What to use:

In summary we should use a softmax activation for a multi-class or binary classification problem in the output layer. We could use a sigmoid in the output layer for a binary classification problem. If we have a regression problem we should use a linear activation in the output layer. In the hidden layers we should try a ReLU activation but shift to a Leaky ReLU if we experience dead neurons. The ReLU and leaky ReLU should not be used in the output layers for our classification or regression problems. The tanh can be used in the hidden layers but a ReLU is preferred over it.